排序数组(Leetcode 912)

发表于 | 分类于 ， ， ， ， | | 本文总阅读数 次
| 字数统计: 2.6k | 阅读时长 ≈ 10
Leetcode 912

1

题目分析

   这个题目非常简单，初学语言的小伙伴们都应该可以求解。排序也是算法中最基础最核心的问题之一，今天不是讲解这一道题目，而是给小伙伴们讲解常见的十种排序算法，就按照题目的要求，升序排列。

稳定排序和不稳定排序

在排序算法性能的比较中，除了时间复杂度和空间复杂度外，还有一个因素是排序是否稳。什么是稳定呢？简单来说，稳定是两个相同的数字不会因为排序算法而导致顺序调换，如1，3(1)，5，3(2)排序后为1，3(2)，3(1)，5，本来第一个3和第二个3交换了顺序，那么这个排序就是不稳定的。对于纯数字来说，稳定和不稳定没有太大意义，但是如果对于某个类，将某个属性进行排序，则就非常有必要了。举个例子，有100个人到银行排队，它们都是普通客户，这时候来了一个VIP客户，这时需要对数据进行排序，将VIP客户的优先级提高，但是如果排序是不稳定的，则后面100个人的顺序将会被打乱，这时，之前排在第一个的人肯定是不愿意的。这就是不稳定排序造成的后果。

冒泡排序

bubble
冒泡排序可能是我们最早接触的排序算法之一了，什么是冒泡排序呢？比较相邻的两个数值，如果前一个数大于后一个数，则交换两个数，就像吐泡泡一样，每一轮迭代会将最大的数放在最后，而且可以添加一个监视器，如果某一轮迭代都没有发生任何依次交换，说明这个序列已经是有序的，则可以提前停止。冒泡排序算法的时间复杂度为$O(n^2)$，最好情况为$O(n)$，最坏情况为$O(n^2)$，空间复杂度$O(1)$，稳定排序。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def bubble_sort(self, nums):
        for i in range(len(nums) - 1):
             # 改进后的冒泡，设置一个交换标志位
            flag = False 
            for j in range(len(nums) - i - 1):
                if nums[j] > nums[j + 1]:
                    nums[j], nums[j + 1] = nums[j + 1], nums[j]
                    flag = True
            if not flag:
                return nums
        return nums

选择排序

select
选择排序思路也非常简单，每次从剩余数组中选择一个最小的放在当前位置上，选择排序算法的时间复杂度为$O(n^2)$，最好情况为$O(n^2)$，最坏情况为$O(n^2)$，空间复杂度$O(1)$，不稳定排序。

1
2
3
4
5
6
7
8
9
10
class Solution:
    def selection_sort(self, nums):
        for i in range(len(nums)):
            min_idx = i
            for j in range(i + 1, len(nums)):
                if nums[min_idx] > nums[j]:
                    min_idx = j

            nums[i], nums[min_idx] = nums[min_idx], nums[i]
        return nums

插入排序

insert
插入排序类似于冒泡排序，插入排序保证当前位置以前的都是有序的，将当前位置从后向前通过交换的方式，插入到之前有序的位置中，插入排序算法的时间复杂度为$O(n^2)$，最好情况为$O(n)$，最坏情况为$O(n^2)$，空间复杂度$O(1)$，稳定排序。

1
2
3
4
5
6
7
8
9
10
class Solution:
    def insertion_sort(self, nums):
        # 第一层for表示循环插入的遍数
        for i in range(1, len(nums)):
            for j in range(i, 0, -1):
                if nums[j] < nums[j - 1]:
                    nums[j], nums[j - 1] = nums[j - 1], nums[j]
                else:
                    break
        return nums

快速排序

quick
快速排序是一种面试常问的排序方法，其思想是每次选择一个基准值，将小于等于基准值的放在左边，大于基准值的放在右边，然后递归左边和右边两个子序列，快速排序算法的时间复杂度为$O(nlog(n))$，最好情况为$O(nlog(n))$，最坏情况为$O(n^2)$，空间复杂度$O(log(n))$，不稳定排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def quick_sort(self, nums):

        def quicksort(nums, begin, end):
            if begin < end:
                base_element, head, tail = nums[begin], begin, end
                while head < tail:
                    while head < tail and nums[tail] > base_element:
                        tail -= 1
                    while head < tail and nums[head] <= base_element:
                        head += 1
                    nums[head], nums[tail] = nums[tail], nums[head]
                nums[tail], nums[begin] = nums[begin], nums[tail]
                quicksort(nums, begin, head - 1)
                quicksort(nums, head + 1, end)
        quicksort(nums, 0, len(nums) - 1)
        return nums

归并排序

merge
归并排序利用了一种分治的思想，先对序列进行分解，分解成长度为1的n个子序列，这n个子序列因为长度为1，故都是有序的，然后再进行合并，合并的时候就是两个有序数组进行合并，因此排序速度会大大提升，归并排序算法的时间复杂度为$O(nlog(n))$，最好情况为$O(nlog(n))$，最坏情况为$O(nlog(n))$，空间复杂度$O(n)$，稳定排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def merge_sort(self, nums):

        def merge(nums, begin, mid, end):
            new_list = []
            p_1, p_2 = begin, mid + 1
            while p_1 <= mid and p_2 <= end:
                new_list, p_1, p_2 = [new_list + [nums[p_1]], p_1 + 1, p_2 + 0] if nums[p_1] <= nums[p_2] else [new_list + [nums[p_2]], p_1 + 0, p_2 + 1]
            new_list += nums[p_2:end + 1] if p_1 > mid else nums[p_1:mid + 1]
            nums[begin:end + 1] = new_list

        def mergesort(nums, begin, end):
            if begin < end:
                mergesort(nums, begin, (begin + end) // 2)
                mergesort(nums, (begin + end) // 2 + 1, end)
                merge(nums, begin, (begin + end) // 2, end)

        mergesort(nums, 0, len(nums) - 1)
        return nums

桶排序

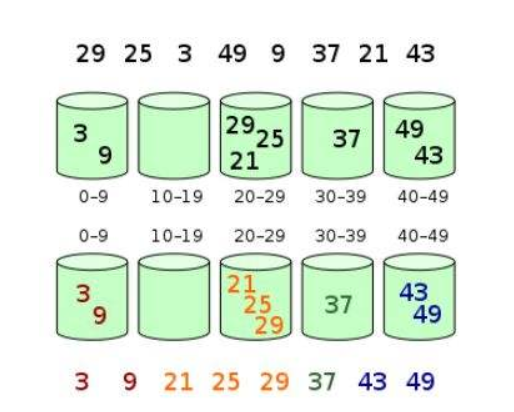
bucket
桶排序首先建立k个桶，每个桶有一定的范围，将原始序列分桶装入，这样排序时只要每个桶是有序的，则整体是有序的，可以降低时间复杂度。桶排序算法的时间复杂度为$O(n + k)$，最好情况为$O(n + k)$，最坏情况为$O(n^2)$，空间复杂度$O(n + k)$，稳定排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def bucket_sort(self, nums):
        min_num = min(nums)
        max_num = max(nums)
        # 桶的大小
        bucket_range = (max_num - min_num) / len(nums)
        # 桶数组
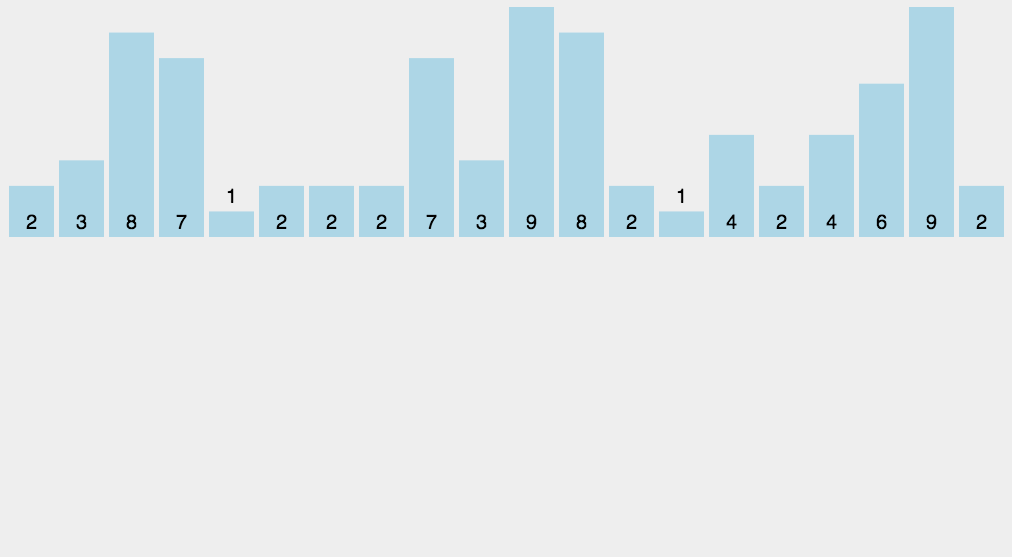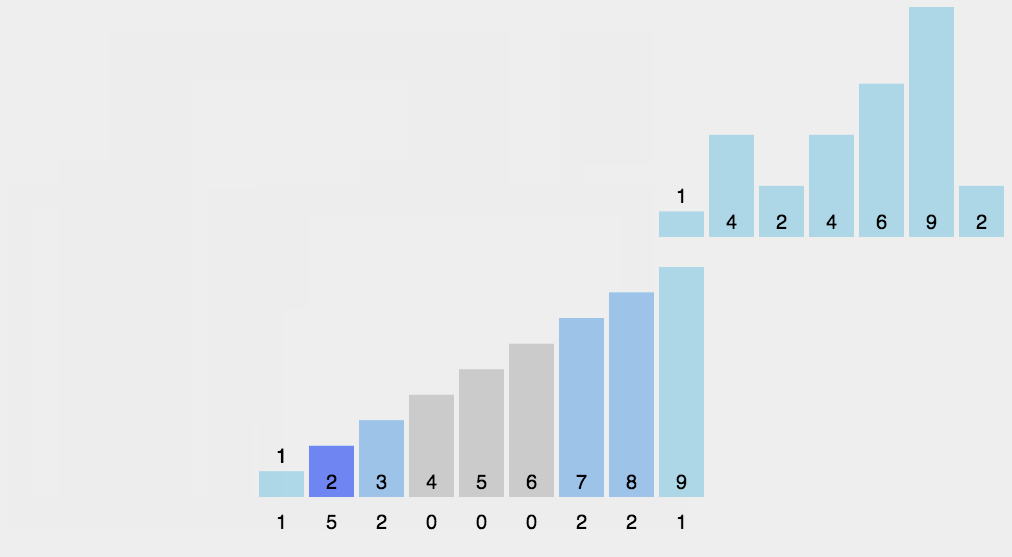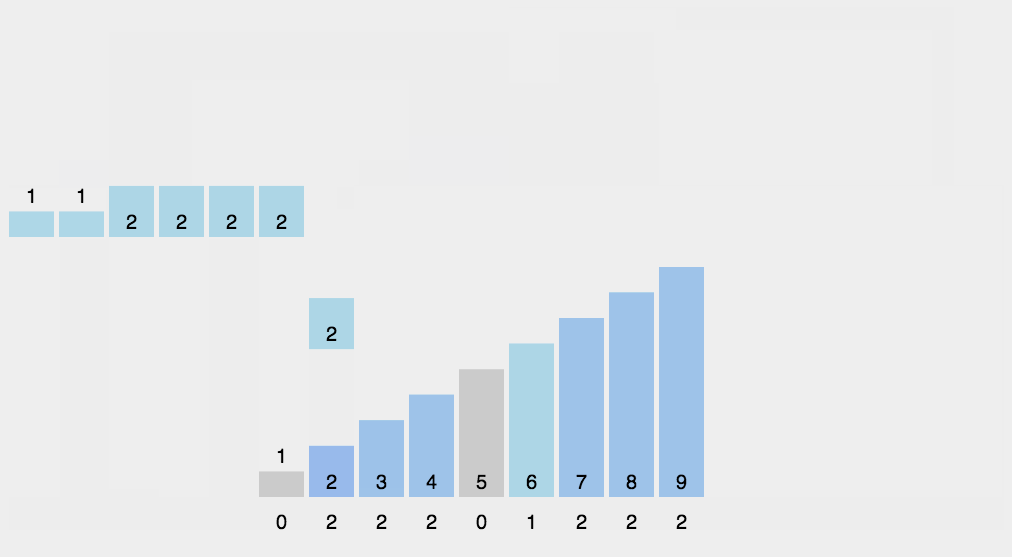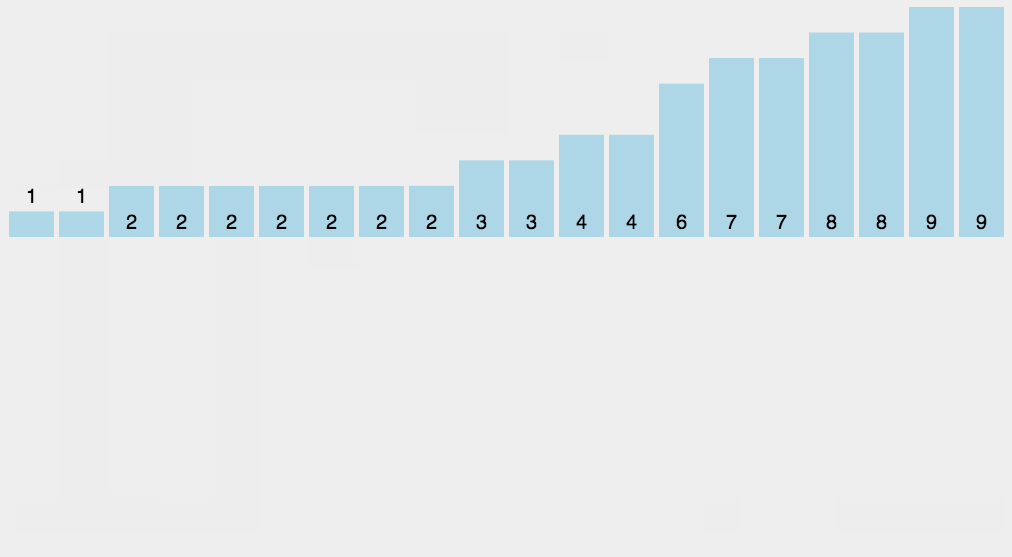
        count_list = [[] for i in range(len(nums) + 1)]
        # 向桶数组填数
        for i in nums:
            count_list[int((i - min_num) // bucket_range)].append(i)
        nums.clear()
        # 回填，这里桶内部排序直接调用了sorted
        for i in count_list:
            for j in sorted(i):
                nums.append(j)
        return nums

计数排序

count
计数排序的原理也很简单，用数组下标统计元素出现的个数即可，因为数组下标是升序排列的，因此输出时只需要按照数组下标顺序依次输出即可，缺点也很明显，对非整数数组进行排序不太方便。计数排序算法的时间复杂度为$O(n + k)$，最好情况为$O(n + k)$，最坏情况为$O(n + k)$，空间复杂度$O(n)$，稳定排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def count_sort(self, nums):
        # 找到最大最小值
        min_num = min(nums)
        max_num = max(nums)
        # 计数列表
        count_list = [0] * (max_num - min_num + 1)
        # 计数
        for i in nums:
            count_list[i - min_num] += 1
        nums.clear()
        # 填回
        for ind, i in enumerate(count_list):
            while i != 0:
                nums.append(ind + min_num)
                i -= 1
        return nums

希尔排序

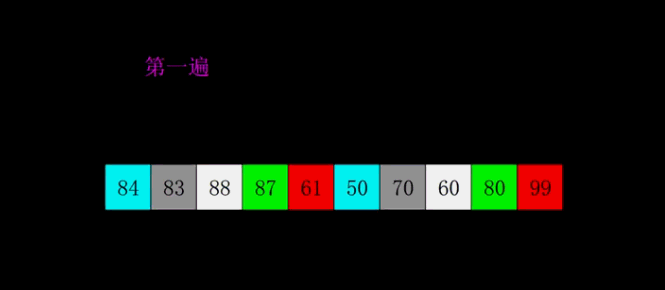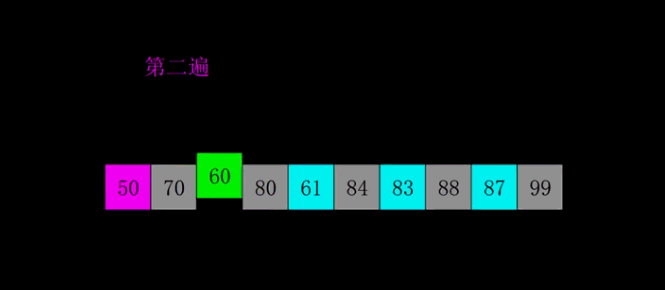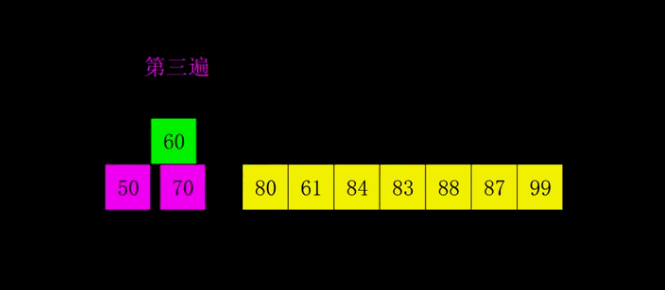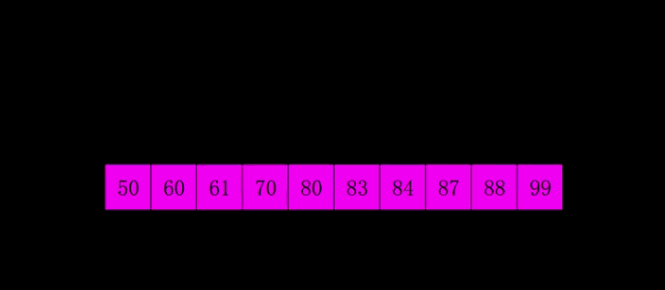
shell
希尔排序类似于插入排序，但是不同点是插入排序增量为1，要插入的值从后向前，一个一个比较，而希尔排序是从后向前有间隔的比较，间隔不同时间复杂度不同，一般按照总长度二分的方式设置间隔。希尔排序算法的时间复杂度为$O(n^{1.3})$，最好情况为$O(n)$，最坏情况为$O(n^2)$，空间复杂度$O(1)$，不稳定排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    def shell_sort(self, nums):
        # 初始步长设置为总长度的一半
        gap = len(nums) // 2
        while gap:
            for i in range(gap, len(nums)):
                # 在每一组里面进行直接插入排序
                for j in range(i, gap - 1, -gap):
                    if nums[j] < nums[j - gap]:
                        nums[j], nums[j - gap] = nums[j - gap], nums[j]
                    else:
                        break
            # 更新步长
            gap //= 2
        return nums

堆排序

heap
堆排序使用了最大堆的概念，指父节点的值大于孩子节点的值，首先建立一个最大堆，然后交换最后一个元素与堆顶元素的值，接着对最大堆进行下沉操作，如果交换进去的值小于孩子节点，则使其下沉，更新最大堆，然后继续交换得到第二大的值，并重复上面的操作即可得到升序的数组。堆排序算法的时间复杂度为$O(nlog(n))$，最好情况为$O(nlog(n))$，最坏情况为$O(nlog(n))$，空间复杂度$O(1)$，不稳定排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def heap_sort(self, nums):

        def heapify(arr, n, i):
            largest = i
            left = 2 * i + 1
            right = 2 * i + 2
            if left < n and arr[i] < arr[left]:
                largest = left
            if right < n and arr[largest] < arr[right]:
                largest = right
            if largest != i:
                arr[i], arr[largest] = arr[largest], arr[i]
                heapify(arr, n, largest)

        n = len(nums)
        # 创建一个长度为n的最大堆
        for i in range(n, -1, -1):
            heapify(nums, n, i)
        for i in range(n - 1, 0, -1):
            # 将大顶堆的堆顶元素和最后一个元素交换
            nums[i], nums[0] = nums[0], nums[i]
            # 创建一个长度为n - 1的最大堆
            heapify(nums, i, 0)
        return nums

基数排序

radix
基数排序类似于桶排序和计数排序，这个排序方式先设置10个桶，按照十进制位进行排序，先排个位，将个位按照升序放入桶内，然后将桶内的数字依次取出，然后排十位，百位，依次下取直到最高位为止，最后将最高位排序后的元素从桶内依次取出即可完成升序排列，缺点和计数排序相同，对非整数数组进行排序不太方便。基数排序算法的时间复杂度为$O(nk)$，最好情况为$O(nk)$，最坏情况为$O(nk)$，空间复杂度$O(n)$，稳定排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def radix_sort(self, nums):
        # 记录当前正在排哪一位，最低位为1
        i = 0
        j = len(str(max(nums)))
        while i < j:
            # 初始化桶数组
            bucket_list = [[] for _ in range(10)]
            for x in nums:
                # 找到位置放入桶数组
                bucket_list[(x // (10 ** i)) % 10].append(x)
            nums.clear()
            # 放回原序列
            for x in bucket_list:
                for y in x:
                    nums.append(y)
            i += 1
        return nums

刷题总结

  排序问题是算法经久不衰的考点之一，这十种方法各有利弊，没有绝对的好与不好，只有不同的适用场景罢了，其中最重要的几个排序方法是冒泡排序，快速排序，归并排序，堆排序。由于其面试出题过于频繁，很多公司已经不考这个简单的算法问题，但是小伙伴们也必须要掌握它。

-------------本文结束感谢您的阅读-------------
0%